Artigo desenvolvido com a colaboração de Leonardo Gonçalves
Neste artigo falaremos sobre o teste t e o teste de Mann-Whitney para amostras independentes, muito utilizados na produção acadêmica e científica.
Suponhamos que um fabricante de pilhas queira trocar a fórmula dos componentes do seu produto na expectativa de garantir maior durabilidade. Antes de iniciar a produção em larga escala, o fabricante sabe que necessita de informações precisas para garantir que a nova fórmula realmente fará com que a pilha apresente maior durabilidade.
Suponhamos ainda que o fabricante pegou 10 unidades da pilha produzida com a fórmula antiga (pilha A) e 10 unidades produzidas com a nova fórmula (pilha B). Em seguida registrou a durabilidade de cada uma delas, calculou a média e identificou que a durabilidade média da pilha B é maior que a durabilidade média da pilha A.
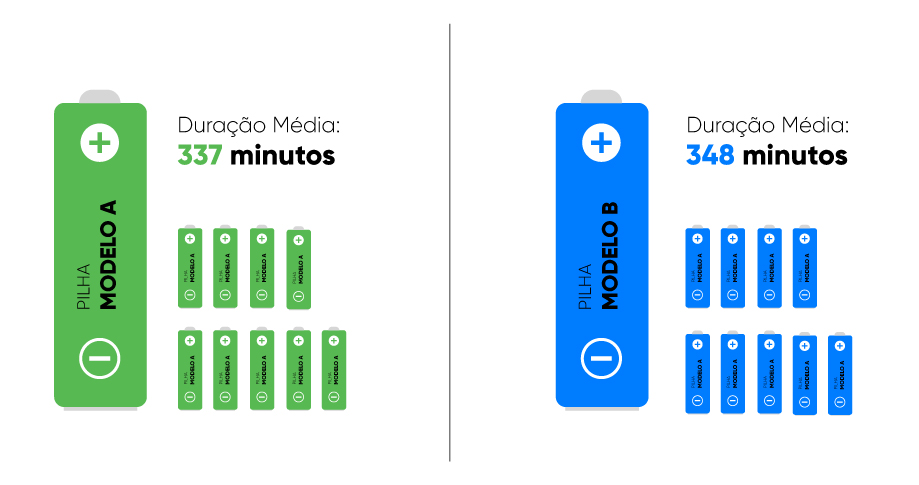
Essa informação é suficiente para concluir que a nova fórmula tem melhor desempenho?
Não! O experimento feito pelo fabricante demonstra somente que, naquela amostra, a pilha B apresentou um melhor desempenho que a pilha A. Mas, será que em uma amostra diferente, com outras 10 unidades de cada pilha, o resultado seria o mesmo? Ou essa diferença se deu pela variabilidade natural do tempo de duração das pilhas? Como então o fabricante poderia verificar se realmente existe diferença significativa entre a durabilidade dos dois modelos de pilhas?
Testes de hipóteses
Para isso existem os testes de hipóteses – eles permitem chegar a conclusões acerca de uma população levando em consideração apenas uma amostra dela. No caso do fabricante, seria necessário utilizar um teste de hipóteses para testar se existe diferenças significativas na duração das pilhas.
Os testes estatísticos usuais são divididos em dois conjuntos principais: paramétricos e não-paramétricos. As técnicas paramétricas, que são mais conhecidas, exigem a suposição de uma distribuição de probabilidade para a população testada. O fabricante teria que verificar ou assumir que, por exemplo, a duração média das pilhas apresenta distribuição normal.
Já os testes não-paramétricos exigem pouca ou nenhuma suposição sobre a distribuição populacional dos dados.
Teste t – Teste Paramétrico
De forma paramétrica, o fabricante poderia comparar as médias das durabilidades das duas pilhas através do teste t ou teste z. Estes testes pressupõem a distribuição normal da população, ou seja, os tempos de duração de uma pilha são igualmente distribuídos ao redor da média. O teste t, em comparação ao teste z, é mais recomendando quando o tamanho amostral é pequeno.
Um importante resultado na Estatística, o Teorema Central do Limite, garante que quando o tamanho da amostra é “grande” o suficiente, a média amostral segue uma distribuição normal. Dessa forma, os testes paramétricos funcionam muito bem para grandes amostras. Como o comportamento da distribuição normal é amplamente conhecido na literatura, se torna possível a estimação de probabilidades a partir de medidas como a média e o desvio-padrão.
Entretanto, em muitos problemas práticos, nem sempre é possível conseguir grandes tamanhos amostrais e os dados podem apresentar distribuições assimétricas, inviabilizando a utilização do teste t. Nesses casos, a utilização das técnicas não-paramétricas pode ser muito útil.
Mann-Whitney – Teste Não-Paramétrico
O fabricante poderia comparar as medianas das durabilidades das duas pilhas através do teste de Mann-Whitney. Os testes não paramétricos são baseados nas posições das observações e não em suas grandezas numéricas. Por isso que se diz que o teste Mann-Whitney compara a mediana ao invés da média (como no teste t). Além disso, o teste de Mann-Whitney não faz nenhuma suposição quanto a distribuição, populacional.
Testar a mediana ao invés da média pode ser muito vantajoso. Conforme pode ser observado nos gráficos abaixo, para distribuições simétricas, média e medianas serão iguais ou muito próximas enquanto que no gráfico com distribuição assimétrica a mediana está mais próxima da “massa de dados” do que a média. Nesse caso a mediana é uma medida de informação mais eficiente que a média, uma vez que não é sensível a valores extremos.
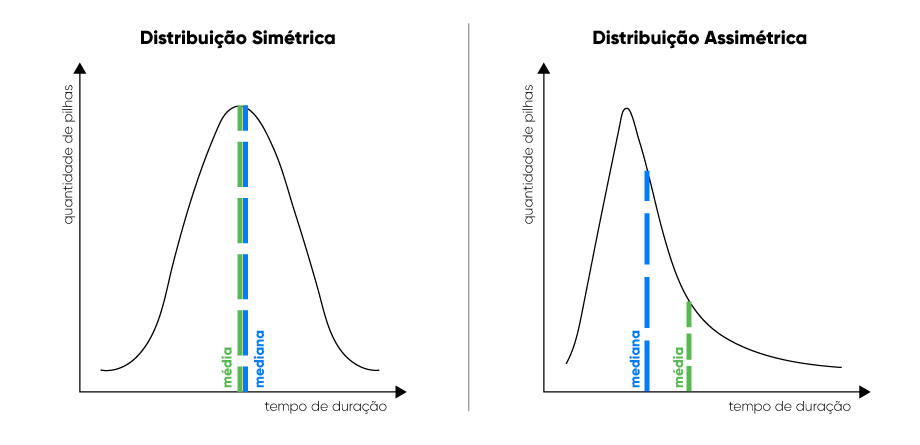
Para conseguir testar de maneira eficiente se a pilha B produzida com a nova fórmula tem duração maior que a pilha A, o fabricante precisa estar atento ao tamanho amostral utilizado e à distribuição de probabilidade da durabilidade das pilhas na hora de decidir qual teste estatístico utilizar, se utiliza o teste t ou Mann-Whitney.
A aplicação de um teste de hipótese para testar diferença entre duas amostras independentes pode não ser tão trivial quanto parece e exige atenção à certos detalhes sobre as amostras. Na dúvida, tenha em conta que o teste Mann-Whitney é mais conservador e versátil que o teste t, já que não exige nenhuma suposição sobre a distribuição dos dados, mas também que se perde informação, uma vez que é baseado nas posições das observações e não em suas grandezas numéricas.
Existem outras metodologias e modelos estatísticos que poderiam ser aplicados à resolução do problema do fabricante, como análise de confiabilidade e tempo de falha utilizando modelos de regressão, tema sobre o qual poderemos escrever no futuro. Por esse motivo, não deixe de nos seguir no Instagram, LinkedIn e Facebook para acompanhar nossas publicações.




5 comentários em “Teste t e Mann-Whitney para amostras independentes”
Parabéns gostei do conteúdo.
–
Realmente hoje no marketing digital temos que ficar
sempre antenados as novidades do mercado,
acompanhando tudo que aparece para somar em nossas
estratégias.
–
Vou ficar acompanhando o site para mais notícias como
essa.
–
Abraços.
boa matéria, bem esclarecedora !!
Valeu, Bruno!
Excelente explicação!
Valeu Jhonnatas!