Artigo desenvolvido com a colaboração de Leonardo Gonçalves
A Regressão de Poisson, também conhecida como Modelo Log-Linear de Poisson, faz parte da família de Modelos Lineares Generalizados (GLM) e é adequada para a modelagem de variáveis que envolvam dados de contagem ou taxas.
Pode ser utilizada para modelar, por exemplo, o número de acidentes em uma rodovia por dia, o número de gols na primeira fase do campeonato Brasileiro, o número de produtos vendidos por dia em uma loja, etc.
A Regressão Linear Simples, que faz uso da suposição de normalidade, não é adequada na modelagem de variáveis como as descritas acima, uma vez que essas são de caráter discreto e não assumem valores negativos – não existe “meio-gol” ou número de gols negativos.
Como uma característica de Modelo Linear Generalizado (GLM), a Regressão de Poisson utiliza a função de ligação “log”, a fim de possibilitar a interpretação dos resultados.
Controlando Variáveis de Contagem
As contagens muitas vezes precisam ser controladas por alguma característica da população de origem. Por exemplo, suponhamos que se deseja analisar o número de sanduíches vendidos em dois restaurantes de uma mesma franquia. Entretanto, o primeiro restaurante possui 20 funcionários, enquanto o segundo possui apenas 7.
Dessa forma, é melhor analisar o número de sanduíches vendidos controlando pelo número de funcionários, que é uma característica que denota a dimensão das lojas.
Exemplo de Aplicação: Incidência de Câncer de Pele Não Melanoma
Para ilustrar a aplicação da Regressão de Poisson, utilizaremos uma base de dados conhecida no meio científico que busca avaliar a incidência de câncer de pele não melanoma em mulheres em duas regiões dos Estados Unidos.
A primeira, Minneapolis-St Paul, é a área urbana mais populosa do estado de Minnesota, localizada na região Centro-Norte do país. A temperatura anual média no aeroporto internacional de Minneapolis–St. Paul é de 7,4 ºC.
A segunda região, Dallas-Fort Worth, é a maior área metropolitana do Sul dos EUA. Fort Worth, a segunda maior cidade da região, tem clima subtropical úmido. O mês mais quente (julho) apresenta temperatura média de 28,9 º C e o mês mais frio (janeiro) de 6º C.
O câncer de pele do tipo não melanoma é o tipo de câncer mais frequente sendo responsável por mais de 90% de todos os cânceres de pele. É também o que apresenta menor taxa de mortalidade, devido aos altos percentuais de cura quando detectado precocemente.
A tabela abaixo apresenta um resumo dos casos de câncer não melanoma em mulheres nas duas regiões por faixa etária. É possível observar uma tendência crescente no número de casos por faixa etária. Ainda, em números absolutos, a região de Dallas – Ft. Worth apresenta maior número de casos que a região Minneapolis – St. Paul, o que poderia se esperar devido as diferenças geoclimáticas entre as regiões.
| Faixa Etária | Minneapolis – St. Paul | Dallas – Ft. Worth | ||
| Nº de Casos | População | Nº de Casos | População | |
| 15 – 24 | 1 | 172.675 | 4 | 181.343 |
| 25 – 34 | 16 | 123.065 | 38 | 146.207 |
| 35 – 44 | 30 | 96.216 | 119 | 121.347 |
| 45 – 54 | 71 | 92.051 | 221 | 111.353 |
| 55 – 64 | 102 | 72.051 | 259 | 83.004 |
| 65 – 74 | 130 | 54.722 | 310 | 55.932 |
| 75 – 84 | 133 | 32.185 | 226 | 29.007 |
| 85+ | 40 | 8.328 | 65 | 7.582 |
Inclusão de Offset
Como o tamanho da população por região e por faixa etária é diferente, não podemos analisar o número de casos de câncer isoladamente. Dessa forma, para o ajuste da Regressão de Poisson, deve haver a inclusão de uma componente do modelo, chamada offset, que é responsável por controlar o número de casos de câncer pela população em cada uma das faixas.
Como uma característica do modelo, o offset é incluído em escala logarítmica, para estar de acordo com a função de ligação utilizada.
Modelo de Regressão Log-Linear de Poisson
A tabela abaixo mostra o ajuste da Regressão de Poisson para o número de casos de câncer de pele não melanoma, utilizando a população como offset. É possível observar que houve diferença significativa (valor-p=0,000) entre as regiões, sendo que a incidência de câncer de pele não melanoma foi 2,23 [2,02; 2,47] vezes maior na região Dallas-Fort Worth, quando comparada a região Minneapolis-St Paul.
Além disso, houve diferença significativa (valor-p=0,000) das faixas etárias sobre a incidência de câncer de pele, sendo que quanto mais velhos os indivíduos, maior a incidência de câncer de pele não melanoma. Por exemplo, em comparação a faixa etária (15-24), a incidência foi 13,87 [19,24; 114,07] vezes maior na faixa etária (25-34) e 482,03 [196,82; 1180,53] vezes maior na faixa etária (85+).
| Variáveis | β | E.P.(β) | Exp(β) | I.C.-95% | P-valor |
| Intercepto | -11,66 | 0,45 | – | – | 0,000 |
| Região=Minneapolis-St Paul | – | – | 1,00 | – | – |
| Região= Dallas-Fort Worth | 0,80 | 0,05 | 2,23 | [2,02; 2,47] | 0,000 |
| Idade (15-24) | – | – | 1,00 | – | – |
| Idade (25-34) | 2,63 | 0,47 | 13,87 | [5,55; 34,65] | 0,000 |
| Idade (35-44) | 3,85 | 0,45 | 46,85 | [19,24; 114,07] | 0,000 |
| Idade (45-54) | 4,60 | 0,45 | 98,99 | [40,90; 239,60] | 0,000 |
| Idade (55-64) | 5,09 | 0,45 | 161,90 | [67,02; 391,11] | 0,000 |
| Idade (65-74) | 5,65 | 0,45 | 282,87 | [117,33; 682,01] | 0,000 |
| Idade (75-84) | 6,06 | 0,45 | 427,52 | [176,97; 1032,77] | 0,000 |
| Idade (85+) | 6,18 | 0,46 | 482,03 | [196,82; 1180,53] | 0,000 |
Equação do Modelo de Regressão Poisson
Sendo g(X) a função de ligação, a equação do modelo é dada por:
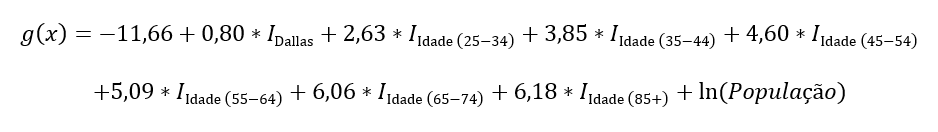
“IDallas“ recebe 1 quando a região é Dallas-Fort Worth e 0 quando a região é Minneapolis-St Paul, “IIdade(25-34)“ recebe 1 quando a faixa etária é (25-34) e 0 para as demais faixas, etc.
Para calcular o número de casos de câncer não melanoma esperado/estimado pelo modelo, é necessário aplicar uma função inversa a função de ligação, sendo representada por:
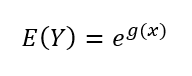
Por exemplo, o número esperado/estimado pelo modelo para a região de Minneapolis-St Paul para a faixa etária de (55 – 64) é 100,90, sendo que o valor real foi de 102 casos. O número esperado/estimado para a mesma faixa etária e para a região de Dallas-Fort Worth é de 225,46 casos, sendo que o valor real foi de 259.
Fenômeno de Subdispersão e Superdispersão na Regressão de Poisson
Na teoria da Probabilidade, a distribuição de Poisson é conhecida por assumir que média e variância são iguais a uma taxa λ. Todavia, em casos reais, a variância dos dados pode ser menor ou maior que a média, causando no modelo os problemas de subdispersão ou superdispersão.
Uma maneira prática de testar este problema é a razão simples entre a média e a variância da dimensão de interesse. Caso o valor seja maior que 1, os dados são subdispersos e, caso o valor seja menor que 1, os dados são superdispersos.
Existem testes formais e adaptações da Regressão de Poisson para absorver a subdispersão ou superdispersão da variável resposta, que poderão ser discutidos em artigos futuros.
Como ajustar uma Regressão de Poisson?
A maioria dos ambientes e softwares de análise estatística possuem recursos para ajustar a Regressão de Poisson. O R, por exemplo, consegue ajustar Modelos Lineares Generalizados a partir do pacote base, usando a função glm().
Gostou do nosso conteúdo? Fique por dentro de todas as novidades do nosso blog seguindo a Oper no Instagram, Facebook e LinkedIn.



6 comentários em “Regressão de Poisson: exemplo de aplicação”
Qual a diferença da regressão de Poisson para uma regressão linear multivariada ?
Oi Tatiana! A Regressão Linear Múltipla é um modelo de análise que usamos quando modelamos a relação linear entre uma variável de desfecho contínua e múltiplas variáveis preditoras que podem ser contínuas ou categóricas.
A Regressão de Poisson é adequada para a modelagem de variáveis que envolvam dados de contagem ou taxas. Por exemplo, pode ser utilizar para modelo o número de acidentes em uma rodovia por dia, o número de produtos vendidos por dia em uma loja, etc. Já a Regressão Linear Múltipla é um modelo de análise que usamos quando modelamos a relação linear entre uma variável de desfecho contínua e múltiplas variáveis preditoras que podem ser contínuas ou categóricas.
Uma diferença é que a suposição de normalidade não é adequada na modelagem de variáveis de contagem (usadas na Regressão de Poisson) já que são de caráter discreto e não assumem valores negativos.
Outra diferença está na interpretação das estimativas. No modelo de regressão linear estamos avaliando o aumento de 1 unidade na variável explicativa, e o quanto espera-se (em média) o acréscimo ou decréscimo na variável resposta. Por exemplo, com o aumento de 1 unidade na variável na idade, espera-se um aumento médio X na variável experiência profissional.
Já na regressão de Poisson, estamos avaliando quantos vezes maior é a incidência da variável resposta com relação as variáveis explicativas. Por exemplo, a incidência de câncer de pele não melanoma foi 2,23 vezes maior na região Dallas-Fort Worth quando comparada a região de Minneapolis-St Paul (exemplo do artigo).
Thanks for sharing. I read many of your blog posts, cool, your blog is very good.