O desvio padrão e o erro padrão são dois conceitos importantes da estatística que têm relevância direta em como você interpreta os dados de forma segura e mais próxima da realidade.
Suponha que um restaurante encomende sucos de laranja de uma cooperativa e sucos de uva de outra cooperativa. Ambas fornecem os sucos em garrafas com capacidade de 500 mililitros.
O dono do restaurante começa então a receber reclamações de seus clientes, alegando que a garrafa de suco consumida tinha menos líquido que o informado. Com isso, ele decide verificar se as cooperativas estão realmente entregando a quantidade correta de suco nas garrafas e pede que um de seus funcionários selecione 10 unidades de cada suco e verifique o volume em um medidor.
Após a verificação, ele observa que as garrafas de ambas cooperativas tinham em média exatamente 500 ml de suco. Ele então supõe que o problema esteja na variabilidade das garrafas, ou seja, umas devem ter mais e outras menos suco. Sendo assim, pede que seu funcionário meça a variabilidade da quantidade de suco nas garrafas de cada cooperativa.
Como fazer, então, a análise de variação da quantidade de suco nas garrafas?
É nesse ponto que entra em questão o cálculo do desvio padrão.
O desvio padrão
Pesquisando sobre como medir o grau de variação entre as amostras, o funcionário descobre que da mesma forma que existem medidas de tendência central como a média e a mediana, existem medidas que podem ser utilizadas para detectar a variabilidade de um conjunto de dados, como a amplitude e o desvio padrão.
O desvio padrão é uma medida que indica a dispersão dos dados dentro de uma amostra com relação à média. Assim, quando se calcula o desvio padrão juntamente com a média de diferentes grupos, obtém-se mais informações para avaliar e diferenciar seus comportamentos.
Sendo assim, seu funcionário decide calcular o desvio padrão das amostras de suco de laranja e de suco de uva. Mas, como fazer isso?
Como calcular o desvio padrão?
Para calcular o desvio padrão, você precisa primeiro calcular a variância em relação à média, outra importante medida de dispersão com muitas aplicações na estatística e na teoria da probabilidade.
Para calculá-la é preciso subtrair cada uma das medidas individuais pela média (passo 1) e elevar os resultados obtidos ao quadrado (passo 2). Em seguida você deverá somar todos resultados (passo 3) e dividir pelo tamanho da amostra menos um (passo 4).
Pronto, já temos a variância! Para se chegar ao desvio padrão basta calcular a raiz quadrada desse resultado (passo 5).

Como interpretar o desvio padrão?
Após calcular os desvios padrão das amostras dos sucos de laranja e de uva, o funcionário apresenta para o dono do restaurante os resultados conforme apresentados na tabela abaixo.
| Amostra | Suco de Laranja |
|---|---|
| Garrafa 1 | 446 ml |
| Garrafa 2 | 450 ml |
| Garrafa 3 | 554 ml |
| Garrafa 4 | 547 ml |
| Garrafa 5 | 486 ml |
| Garrafa 6 | 498 ml |
| Garrafa 7 | 440 ml |
| Garrafa 8 | 560 ml |
| Garrafa 9 | 451 ml |
| Garrafa 10 | 568 ml |
| Média | 500 ml |
| Desvio Padrão | 52,7 ml |
| Amostra | Suco de Uva |
|---|---|
| Garrafa 1 | 506 ml |
| Garrafa 2 | 507 ml |
| Garrafa 3 | 502 ml |
| Garrafa 4 | 498 ml |
| Garrafa 5 | 496 ml |
| Garrafa 6 | 495 ml |
| Garrafa 7 | 492 ml |
| Garrafa 8 | 503 ml |
| Garrafa 9 | 508 ml |
| Garrafa 10 | 493 ml |
| Média | 500 ml |
| Desvio Padrão | 6,0 ml |
Mas o que significam esses desvios padrão de 52,7 e 6?
Ao interpretar o desvio padrão é importante ter em conta que ele assume a mesma medida da unidade amostral, no caso mililitros. Sendo assim, o desvio-padrão do conteúdo das garrafas de suco de laranja é de 52,7 ml e de 6 ml nas de uva.
Um desvio padrão grande significa que os valores amostrais estão bem distribuídos em torno da média, enquanto que um desvio padrão pequeno indica que eles estão condensados próximos da média. Em poucas palavras, quanto menor o desvio padrão, mais homogênea é a amostra.
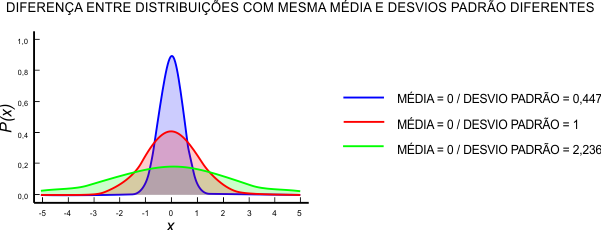
Sendo assim, o dono do restaurante tem uma medida de dispersão capaz de mostrá-lo que o volume das garrafas de suco de laranja varia mais do que no suco de uva.
Mas se o funcionário tivesse selecionado outra amostra de garrafas de suco de laranja e outra amostra de suco de uva a média seria a mesma? Ou a média poderia variar de acordo com a amostra selecionada?
Para resolver essa dúvida temos que analisar o erro padrão da média. Leia mais adiante e descubra como fazer esse cálculo.
O erro padrão
O erro padrão é uma medida de variação de uma média amostral em relação à média da população. Sendo assim, é uma medida que ajuda a verificar a confiabilidade da média amostral calculada.
Para obter uma estimativa do erro padrão, basta dividir o desvio padrão pela raiz quadrada do tamanho amostral. O resultado obtido também estará na mesma unidade de medida do valor amostral.
Seguindo nosso exemplo, com as 10 amostras de cada suco, o erro padrão calculado do volume de suco de laranja nas garrafas foi de 16,7 ml e do volume de suco de uva foi 1,9 ml.
Como podemos utilizar o erro padrão?
Através do erro padrão, pode-se estimar um intervalo de confiança para a média populacional a partir da média amostral calculada. Nesse contexto, o funcionário não precisa abrir centenas de garrafas para verificar como as médias de diferentes amostras podem variar, ele pode utilizar o erro padrão e um nível de significância.
Com um nível de significância de 5%, por exemplo, pode-se construir um intervalo de confiança que terá 95% de probabilidade de conter a média real de líquido presente nas garrafas de suco de laranja.

Erro padrão e intervalo de confiança
Para calcular o intervalo de confiança basta multiplicar o erro padrão pelo percentil associado ao nível de significância observado em uma distribuição normal padrão, ou seja, que apresenta média 0 e desvio-padrão igual a 1.
Para o nível de significância de 5%, esse valor é de 1,96. Portanto, o dono do restaurante pode ter em conta que existe a probabilidade de 95% do intervalo de 467,4 a 532,6 mililitros (500 ± 1,96 * 16,7) conter a média do volume das garrafas de suco de laranja.
Da mesma forma, pode afirmar que o intervalo entre 496,3 e 503,7 ml (500 ± 1,96 * 1,9) tem probabilidade de 95% de conter a média do suco de uva presente nas garrafas.
A diferença entre desvio padrão e erro padrão
É muito frequente a confusão entre os conceitos de erro padrão e desvio padrão. Apesar de ambos tratarem sobre a variação da média, são conceitos bem diferentes entre si.
O desvio padrão, como vimos, trata de um índice de dispersão da amostra em relação à média, enquanto o erro padrão é uma medida que ajuda a avaliar a confiabilidade da média calculada.
Agora que você já é capaz de diferenciar desvio padrão de erro padrão, não deixe de se registrar em nosso Blog e acompanhar nossas futuras publicações . Caso tenha ficado alguma dúvida, não hesite em entrar em contato com nossos Data Talkers.





35 comentários em “O que é Desvio Padrão e Erro Padrão?”
Olá!
A explicação está ótima mas é preciso rever o quadro de cálculo do desvio padrão pois os valores não condizem com os resultados. Grato!
Oi Carlos, já corrigimos o quadro de cálculo do desvio padrão. Obrigada pelo feedback!
Olá! Fiquei um pouco confusa na parte:
“Da mesma forma, pode afirmar que o intervalo entre 496,3 e 503,7 ml (500 ± 1,96 * 1,9) tem probabilidade de 95% de conter o média do suco de uva presente nas garrafas.”
A probabilidade não seria algo booleano – a média populacional está ou não está dentro do intervalo (sim/não) -, enquanto que na verdade esse 95% referem-se que, se repetirmos esse procedimento 100 vezes onde o funcionário calcula a média das 10 garrafas, nas 95 vezes teremos o a média dentro do intervalo?
Oi Maria Eduarda, talvez o texto não tenha ficado muito claro, mas foi exatamente o que você disse que nós queríamos dizer!
Exato Maria! A média populacional ou está ou não está no intervalo calculado. Os 95% se referem a quantidade esperada de intervalos que conterão este verdadeiro valor a medida que o processo de amostragem tende ao infinito.
Parabéns pelo blog! Conteúdo muito explicativo, ficou bem fácil o entendimento!!
Obrigada Mariana 🙂 Segue a gente nas redes sociais para ficar sempre por dentro de tudo!
Parabéns! Explicação muito clara!
Obrigado.
Obviamente foi bom ler e compreender o que esta escrito.
Necessitarei de outras oportunidades para interagir, gostei da matéria.
A: Memwana
Parabéns pelo ótimo site. Muito bom mesmo. Sucesso nas publicações…
Adorei seu conteúdo Parabéns, bem completo e dinâmico.
Era exatamente o que eu estava buscando na internet e
todas as minhas dúvidas foram tiradas aqui. Muito sucesso e
gratidão!
Boa tarde. O intervalo de confiança para as garrafas de suco de laranja vai de 467,3 a 532,6. E para as garrafas de suco de uva? O percentil associado ao nível de significância é o mesmo (1,96)? Usando a função int.confiança no LibreOffice Calc cheguei aos valores 496,10 e 503,90. Está correto?
Sim, está correto! Os valores calculados pelo LibreOffice Calc estão corretos, tem apenas uma diferença de décimos que deve ter acontecido pelos arredondamentos. No artigo usamos 1,965 e você deve ter usado 1,96, mas os dois estão certos.
Explicação incrível!
Parabéns!!!
Valeu Daiana!
Para cálculo da variância, a divisão não seria pelo número de elementos? Ao invés do número de elementos menos um?
Boa pergunta! E a resposta para ela é sim e não! Quando queremos o desvio-padrão populacional dividimos pelo número da população. E quando queremos calcular o desvio-padrão amostral, aí sim, dividimos pelo número da amostra menos um.
Rafael, acho que essa é a primeira dúvida que aparece quando a gente fala de variância amostral. É frequente a estranheza ao ver n-1 no denominador da variância amostral ao invés de n. Isso acontece pq a variância amostra é um estimador para variância populacional (a variância verdadeira dos dados). Se você não tem todos os dados da população alvo do estudo disponíveis, então o que vc tem é uma amostra. Todas as medidas que vc calcula para essa amostra são estimativas das medidas do todo.
O melhor estimador para a média é a própria média, mas isso não acontece com a variância. O melhor estimador para a variância (aquele que é não viesado, consistente e eficiente) é o de denominador n-1. Isso envolve alguns conceitos mais avançados tb, como por exemplo o significado de graus de liberdade.
Adorei! Muito bem explicado! Só faria uma observação… se a amostra for infinita ou se os dados coletados tiverem reposição o divisor do cálculo da variância será pelo total de elementos também! Parabéns pelo texto!
Bom dia, gostei da descrição detalhada, concisa e muito elucidativa. Quero contar convosco numa pesquisa estatística que estou a fazer. Bem haja!
Parabéns pela excelente didática. Fmalmente, Todos os por ques foram esclarecidos! Obrigado
Obrigada, Arlem!
Olá, adorei o post. Gostaria de perguntar, pelo que eu conheço, para se calcular um intervalo de confiança, eu fazia Média +/- Z * DesvioPadrão. No post, vocês usaram Média +/- Z * EPM. Por quê?
Valeu artur! Então, para não entrar nas fórmulas, podemos fazer a seguinte reflexão: um intervalo de confiança teria o mesmo tamanho com uma amostra de tamanho 10 e outra de tamanho 1000 com a mesma média e desvio-padrão? Não, pois o tamanho da amostra impacta no intervalo de confiança calculado.
Isso acontece porque a média amostral segue uma distribuição normal com média equivalente à média populacional e variância igual à variância populacional dividida pelo tamanho da amostra.
Olá ,
“Para o nível de significância de 5%, esse valor é de 1,96.”
Não entendo como chegamos ao valor 1,96 . Olhamos na tabela de distribuição normal? e quando o desvio padrão não é conhecido?
Oi Lorena! Esse valor pode ser encontrado na tabela e depende do nível de significância adotado. Se o teste for bilateral e adotado o nível de significância de 5%, chegamos ao valor de 1,96. Caso o teste seja unilateral, chegamos ao valor de 1,645.
Olá Adilane,
No comentário acima você afirma que “Se o teste for bilateral…” e “Caso o teste seja unilateral…”.
Você poderia explicar melhor esses testes?
Boa tarde, Alex! No caso, o teste bilateral seria para verificar se o desvio padrão está dentro do intervalo: à esquerda para verificar se o desvio padrão é maior que a referência, e à direita para verificar se é menor que a referência. Se a dúvida persistir, pode chamar!
A situacao e o exemo, foram perfeitos para o entendimento. Parabens
Ob rigada pela explicacao. Exemplo muito apropriado para ilustrar os conceitos. Parabens
Nós que agradecemos pelo comentário Celia!
Muito boa a explicação! Obrigada!
Olá! Ótimo conteúdo. No caso, para uma amostra pequena de 10, não seria correto utilizar a tabela t ao invés de usar a tabela Z?
Oi André! Agradecemos a observação. O mesmo vale pra amostras menores que 30 ou 50 (a depender da literatura). Acabamos supondo uma normalidade, mas esquecemos de explicitar isso! Ficaremos mais atentos da próxima vez. Obrigado!
Continuem assim.