Teste de Tukey para Comparações Múltiplas

Quando queremos comparar a distribuição de três ou mais grupos de amostras independentes, geralmente usamos a Análise de Variância ou ANOVA. Após a ANOVA, sabemos que pelo menos um grupo se difere dos demais, mas não sabemos entre quais grupos a diferença é significativa. Para isso, precisamos de um teste de comparações múltiplas, e é aqui que entra o Teste de Tukey!

Para ilustrar a aplicação e utilização do Teste de Tukey, continuaremos utilizando o exemplo fictício apresentado no vídeo sobre “Como interpretar uma Análise de Variância”, porém com alguns dados e resultados diferentes. Nele, se buscava verificar se o desempenho na prova de matemática de alunos de um curso preparatório para o ENEM variava de acordo com o professor que lecionava a disciplina.

No exemplo, os resultados indicaram que existia pelo menos dois professores com alunos com desempenho significativamente diferentes. Agora, utilizaremos o Teste de Tukey para verificar quais são eles.

Leia também: Como interpretar uma Análise de Variância (ANOVA)

O Teste de Tukey

Entre os testes de comparações múltiplas mais utilizados, o Teste de Tukey se destaca por sua potência na comparação entre todos os pares e pela facilidade de aplicação. Também é conhecido como Teste de Tukey HSD (Honestamente Significativa Diferença, na sigla em inglês).

O Teste de Tukey foi desenvolvido por John Wilder Tukey e apresentado em 1949, no artigo intitulado Comparing Individual Means in the Analysis of Variance, publicado na revista Biometrics (vol. 5, n.º 2, p. 99–114. JSTOR 3001913).

Quando os tamanhos amostrais dos grupos são iguais, o Teste de Tukey é considerado um teste exato. Isso significa que, para o conjunto de todas as comparações par a par, a taxa de erro do conjunto dos testes é exatamente igual a α (nível de significância), e os intervalos de confiança são igualmente precisos, com confiança de 1 – α. Vale destacar que testes exatos para comparações múltiplas são raros, já que a maioria não controla adequadamente o nível de significância adotado.

O Teste de Tukey consiste em comparar todos os possíveis pares de médias, baseando-se na Diferença Mínima Significativa (D.M.S.), que considera os percentis do grupo. No cálculo da D.M.S., utiliza-se a distribuição da amplitude estudentizada, o quadrado médio dos resíduos da ANOVA e o tamanho amostral dos grupos.

Fórmula para o Teste de Tukey (D.M.S)

Agora, vamos à fórmula do Teste de Tukey. A diferença mínima significativa, também conhecida como DMS, é calculada usando a seguinte fórmula: ‘Q’ representa o valor crítico de Tukey para o número de grupos e o número total de observações; ‘QMR’ é o quadrado médio do resíduo obtido na análise de variância; e ‘N’ indica o tamanho amostral de cada grupo.

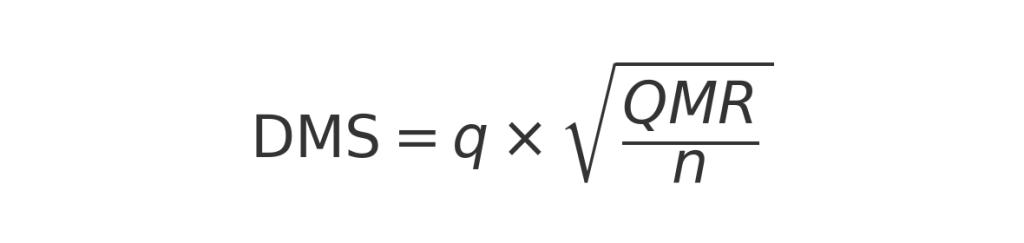
Ela é calculada previamente e indica o menor valor necessário para que uma diferença entre médias seja estatisticamente significativa. Dizemos que uma diferença entre as médias é significativa quando ela é maior do que DMS.

Aplicação do Teste de Tukey (Exemplo Prático)

Para ilustrar a aplicação e utilização do Teste de Tukey, vamos usar um exemplo semelhante ao apresentado no vídeo sobre a interpretação da ANOVA, porém com alguns dados e resultados diferentes. Neste exemplo, queremos verificar se o desempenho na prova de matemática de alunos de um curso preparatório para o ENEM varia de acordo com o professor que leciona a disciplina, com três turmas de 12 alunos cada. Note que, neste caso, existem três comparações par a par a serem realizadas.

Vamos analisar os dados a seguir, onde apresentamos as notas dos alunos de cada professor:

Professor 1:	72, 75, 78, 80, 82, 83, 84, 85, 86, 87, 88, 90
Professor 2:	65, 67, 68, 70, 71, 73, 74, 76, 77, 78, 79, 82
Professor 3:	80, 82, 84, 85, 87, 88, 90, 91, 92, 93, 95, 97

Diferentemente do vídeo sobre ANOVA, neste tutorial apresentaremos uma nova análise com dados específicos. A partir destes dados, calculamos as estatísticas descritivas para cada grupo:

Professor	N	Média	Variância
Professor 1	12	82,50	27,36
Professor 2	12	73,33	26,97
Professor 3	12	88,67	26,06
Total	36	81,50	58,71

Na análise de variância que realizamos, chegamos à seguinte tabela ANOVA:

Fonte de Variação	GL	SQ	QM	F	Valor-p
Tratamento	2	1429,92	714,96	37,69	<0,001
Resíduo	33	626,08	18,97
Total	35	2056,00	58,74

Como podemos ver, o valor F calculado foi 37,69, muito maior que o F crítico (≈ 3,28) para um nível de significância (α) de 5%. Além disso, o p-valor é menor que 0,001, reforçando a rejeição da hipótese nula e indicando que existe pelo menos uma diferença significativa entre as médias dos grupos. Um dado importante nessa tabela é o Quadrado Médio do Resíduo (QMR), identificado como QM, que corresponde a 18,97. Esse valor será essencial para o cálculo do Teste de Tukey.

Nossa análise inicial mostrou que há diferenças significativas no desempenho entre os alunos de diferentes professores. Mas quais professores exatamente? Ou seja, quais grupos diferem entre si? Para saber, utilizaremos o Teste de Tukey para identificar exatamente quais professores têm alunos com desempenhos que realmente se diferenciam.

A Tabela de Tukey

O primeiro passo é calcular a Diferença Mínima Significativa. Para isso, precisamos consultar a Tabela de Tukey. Os valores da tabela são pré-definidos, mas eles podem variar dependendo do número de grupos que estamos comparando e os graus de liberdade do nosso teste. É importante entender que esses valores são padronizados e sempre permanecem os mesmos para as mesmas condições de teste, independentemente dos dados analisados.

No nosso exemplo, queremos comparar três turmas (que representam o nº de grupos) de 12 alunos cada. Somando os três grupos, o número total de alunos é 36, e para calcular os graus de liberdade do erro, usamos a seguinte regra: pegamos o total de alunos e subtraímos pelo número de grupos. Ou seja, 36 – 3 = 33. Esse é o número de graus de liberdade do erro porque estamos analisando a variação dentro de cada grupo e precisamos descontar o número de categorias (neste caso, os professores) da contagem total de dados disponíveis.

Agora que sabemos isso, vamos consultar a Tabela de Tukey.

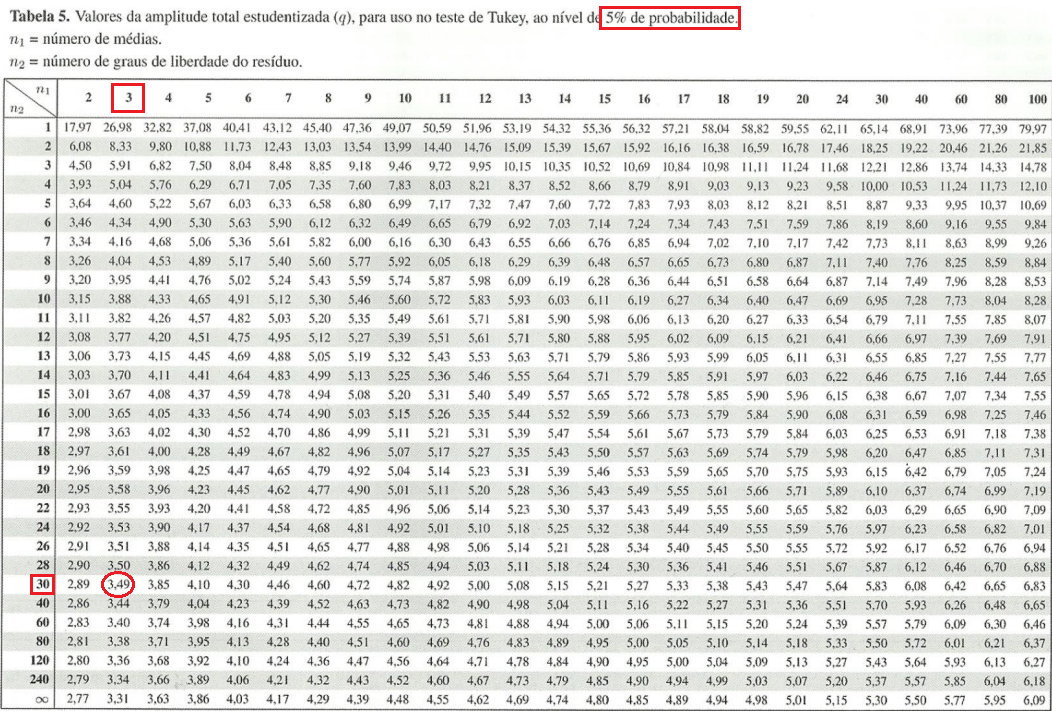
A Tabela de Tukey se baseia em dois valores: o número de médias a serem comparadas (𝑛1, que neste caso é 3) e o número de graus de liberdade do resíduo (identificada como 𝑛2). Como 𝑛2 = 33 não aparece diretamente na tabela, usamos um valor próximo, que é 30. Isso acontece porque as tabelas costumam apresentar apenas alguns valores específicos para facilitar a consulta. Então, utilizaremos o valor correspondente a 30 graus de liberdade, que é 3,49.

Agora, com o valor crítico da Tabela de Tukey e o quadrado médio do resíduo da ANOVA (18,97), podemos calcular a DMS. Esse cálculo determina a menor diferença entre médias que pode ser considerada estatisticamente significativa.

Calculando a Diferença Mínima Significativa

Em nosso exemplo, temos:

• Valor crítico (q) = 3,49
• Quadrado médio do resíduo (QMR) = 18,97
• Número de alunos por grupo (n) = 12

Com esse valor da DMS calculado, vamos agora comparar as médias de cada par de professores. No nosso exemplo, as médias dos alunos por professor são:

• Professor 1: 82,50
• Professor 2: 73,33
• Professor 3: 88,67

Calculando a diferença das médias

Agora, vamos calcular a diferença das médias de cada par de grupos:

Par a par	Diferença das Médias	Resultado
Professor 3 – Professor 1	88,67 – 82,50	6,17
Professor 3 – Professor 2	88,67 – 73,33	15,34
Professor 1 – Professor 2	82,50 – 73,33	9,17

Lembrando que quando a diferença entre duas médias é maior que a DMS, isso indica uma diferença significativa. No nosso caso, a DMS calculada foi de 4,39. Comparando com as diferenças obtidas:

• 6,17 > 4,39 (diferença significativa entre Professor 3 e Professor 1)
• 15,34 > 4,39 (diferença significativa entre Professor 3 e Professor 2)
• 9,17 > 4,39 (diferença significativa entre Professor 1 e Professor 2)

Logo, com esses valores, observamos que o módulo da diferença da média entre todos os pares de professores foi maior que o valor da DMS obtido. Isso nos leva a concluir que o desempenho médio dos alunos dos professores (1 e 2), (1 e 3) e (2 e 3) são significativamente diferentes.

Como interpretar os resultados do Teste de Tukey?

Interpretamos o teste com base na diferença mínima significativa (D.M.S.), no intervalo de confiança e no valor-p:

• Diferença Mínima Significativa: No nosso exemplo, observamos que o módulo da diferença entre as médias dos grupos comparados foi maior que o valor da D.M.S. calculado. Isso nos permite concluir que há diferença significativa entre os desempenhos médios dos grupos analisados: (1 e 2), (1 e 3) e (2 e 3).
• Intervalo de Confiança: Percebemos que o valor 0 (zero) não está presente em nenhum dos intervalos de confiança formados para a diferença entre as médias dos pares. Isso também indica que os grupos (1 e 2), (1 e 3) e (2 e 3) apresentam desempenhos médios significativamente diferentes.
• Valor P: Ao analisarmos os valores-p, notamos que todos são menores que o nível de significância adotado (valor-p < 0,05). Com isso, reforçamos a mesma conclusão obtida anteriormente com a D.M.S. e os intervalos de confiança: os grupos comparados apresentam diferenças estatisticamente significativas entre si.

Como realizar o Teste?

No software R há pelo menos duas maneiras de realizar o Teste de Tukey: através do função TukeyHSD, ou função HSD.test do pacote agricolae. O resultado obtido em ambos os casos é o mesmo, porém em um dos comandos obtém-se o valor do D.M.S, enquanto que no outro tem-se o intervalo de confiança e o valor-p.

Pressupostos para utilização do teste

Mas antes de realizar o teste, você deve garantir que os seguintes pressupostos estejam atendidos:

1. As observações devem ser independentes dentro e entre os grupos.
2. Os grupos precisam seguir uma distribuição normal.
3. A variância dentro dos grupos deve ser constante.

O que fazer quando a suposição da normalidade, por exemplo, não é atendida?

Quando a suposição de normalidade não é atendida, você pode recorrer a procedimentos alternativos à ANOVA e ao Teste de Tukey. Uma opção é aplicar o teste de Kruskal-Wallis para verificar se há diferença entre os grupos. Caso identifique diferenças significativas, você pode utilizar o teste de comparação múltipla de Nemenyi para descobrir quais grupos diferem entre si. Ambos os testes são explicados no artigo Teste de Kruskal-Wallis e Nemenyi.

E quando os tamanhos amostrais dos grupos são diferentes? Devo usar outro teste de comparação múltipla?

Quando os tamanhos amostrais dos grupos são diferentes, você ainda pode usar o Teste de Tukey. Nessa situação, o teste deixa de ser exato e passa a ser uma aproximação. Para isso, aplicamos o Teste de Tukey-Kramer, que adapta a metodologia original ao considerar o tamanho amostral de cada grupo.