Como fazer análise de sobrevivência na prática?

Artigo escrito com a colaboração de Rafael Toledo

A Análise de Sobrevivência é uma área da Estatística caracterizada por estudar o tempo até a ocorrência de um evento de interesse (falha). Ela se desenvolveu justamente pelo avanço e aprimoramento das técnicas estatísticas.

Na área da saúde há muitos estudos com aplicações de análise de sobrevivência devido a sua importância em estimar o tempo de vida de um paciente após o diagnóstico de uma doença. Além disso, é possível estudar o tempo até que o indivíduo possa experimentar o evento de interesse, podendo ser a cura ou recidiva de determinada doença.

Além da área da medicina, a análise de sobrevivência possui aplicações em outras áreas como: engenharia, ciências sociais, negócios e finanças.

Na engenharia estudam-se os produtos ou componentes sob teste para estimar características relacionadas aos seus tempos de vida, o que possibilita definir o planejamento de controle de qualidade, bem como o tempo de garantia/validade de diversos produtos. Denominam esta área de Confiabilidade, pois a interpretação dos resultados se dá através do risco e não do tempo de sobrevida.

Nas ciências sociais, criminalistas estudam o tempo entre a liberação de presos e a ocorrência de crimes, enquanto demógrafos utilizam esta análise para nascimentos, mortes, casamentos, divórcios e migrações. Já as instituições financeiras analisam o tempo até um cliente se tornar inadimplente. 

Qual o objetivo?

O objetivo da análise de sobrevivência pode ser dividido em três:

1. Estimar ou interpretar a função de sobrevivência.
2. Comparar função de sobrevivência e/ou função risco.
3. Avaliar a relação entre variáveis com o tempo de sobrevida.

Quais são as características dos dados de Sobrevivência ?

Os conjuntos de dados de sobrevivência são caracterizados pelos tempos de falha, e regularmente, pelas censuras. Tempos de falha e censura são os dois componentes que constituem a resposta.

Os elementos do tempo de falha são: tempo inicial, escala de medida e o evento de interesse. O tempo deve ser definido com clareza no início, pois o processo de acompanhamento dos estudos se dará a partir da definição desse tempo, inclusive a escala de medida (dias, meses, anos). Os eventos são denominados evento de interesse. Por exemplo, o tempo até a ocorrência da morte do paciente ou falha de um produto eletrônico.

Agora que o tempo de falha e os seus respectivos elementos foram explicados, é necessário entender outro componente dos dados de sobrevivência: a censura.

A censura é determinada pela presença de observações incompletas ou parciais, sendo que o motivo do surgimento de censura pode ser por várias razões. Utilizando um contexto de um estudo clínico, por exemplo, a morte de um paciente por outra causa que não a do estudo, bem como o fim do acompanhamento do indivíduo por alguma razão podem ser fatores que causam a censura.

Por que usamos as censuras nos estudos?

Por mais que as censuras sejam obervações incompletas, possuem relevância por fornecer informações sobre o tempo de vida de pacientes nos estudos sobre doenças, ou o tempo até a falha/defeito de um produto. Vale salientar que a omissão das censuras nos cálculos das estatísticas de interesse podem influenciar nas análises e gerar conclusões enviesadas.

Tipos de Censura

A depender do estudo, há tipos de censura que podem ser ocasionadas ao longo do procedimento. Desta forma, podem ser definidos como censura do tipo I ou do tipo II, aleatória, a direita ou a esquerda e intervalar.

A censura do tipo I ocorre em estudos que ao serem finalizados após um tempo pré-definido, observam-se indivíduos que não experimentaram o evento de interesse. A do tipo II decorre dos estudos finalizados após um número pré-determinado de indivíduos observarem o evento de interesse.

A censura à direita dá-se quando o tempo de registro é menor que a ocorrência do evento, enquanto na censura à esquerda, o evento já ocorreu antes do estudo.

Vale destacar que a censura aleatória ocorre geralmente no campo da medicina, devido ao indivíduo ser retirado durante o estudo sem ter ocorrido a falha. A exemplo disso, morte por causa contrária à estudada.

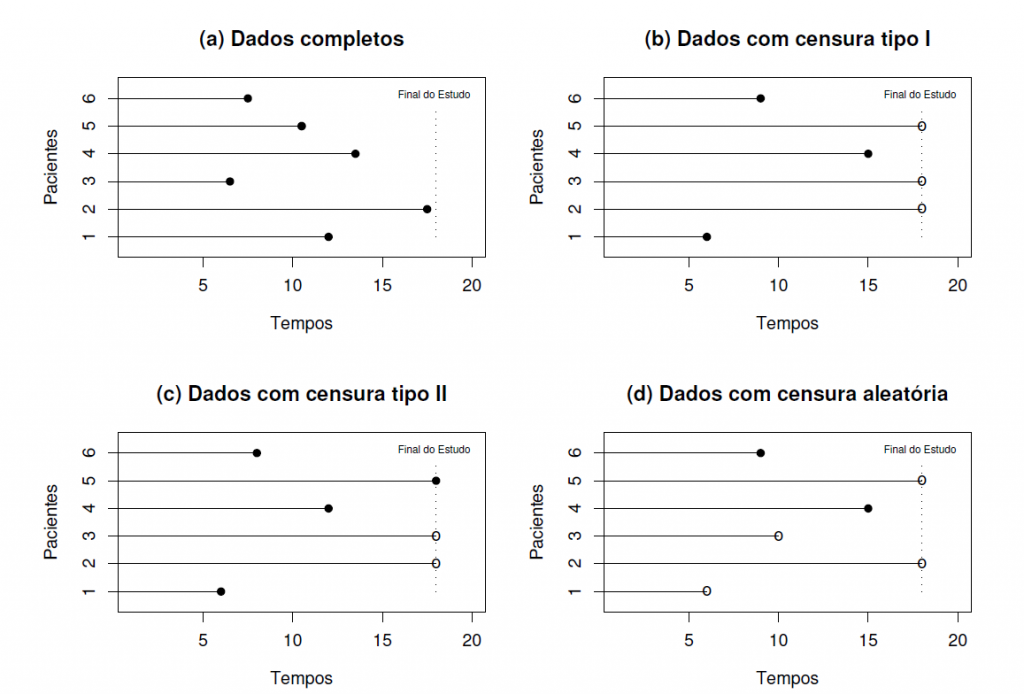
Fonte: Análise de Sobrevivência Aplicada – Colosimo e Giolo.

Note que a imagem acima ilustra os tipos de censura durante um determinado tempo, além do tempo final definido. Em (a) todos os indivíduos experimentaram o evento antes do final do estudo.

Na imagem (b), alguns indivíduos não experimentaram o evento até o final do estudo, enquanto isso, em (c), o estudo foi finalizado após a ocorrência de um número pré-estabelecido de falhas.

A imagem (d) ilustra a censura aleatória, em que o acompanhamento de alguns indivíduos foi interrompido por alguma razão e alguns indivíduos não experimentaram o evento até o final do estudo.

Estimador de Kaplan-Meier

O estimador de Kaplan-Meier é uma técnica estatística não paramétrica para a estimação da função de sobrevivência. É considerado o “padrão-ouro” e baseia-se na ocorrência dos eventos e nas censuras ao longo do tempo.

Esse estimador descreve e compara o comportamento da função de sobrevivência para diferentes grupos de indivíduos (COLOSIMO, E.; SUELY, R., 2006).

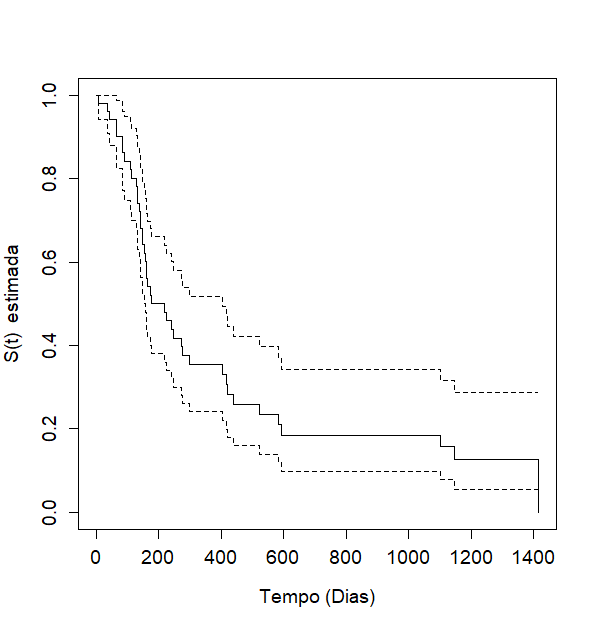
A representação gráfica da função de sobrevivência (a probabilidade de uma observação não falhar até determinado tempo) é denominada curva de sobrevivência, sendo esta uma função escada, e tendo valor constante em cada intervalo de tempo. No caso da imagem acima, note que conforme o tempo aumenta (em dias), a probabilidade de sobrevivência decai. Além disto, é possível comparar essas curvas para determinados grupos e verificar qual grupo possui uma curva de sobrevivência mais acima, ou seja, que a probabilidade de sobrevida decai lentamente durante o tempo.

A imagem abaixo apresenta um exemplo com objetivo de comparar dois tipos de embalagens (A e B) para um certo produto alimentício sem conservante e em temperatura ambiente. Deseja-se investigar se há diferença na durabilidade do referido produto conforme as respectivas embalagens. O evento de interesse é o tempo (em horas) até o produto apresentar problemas na qualidade.

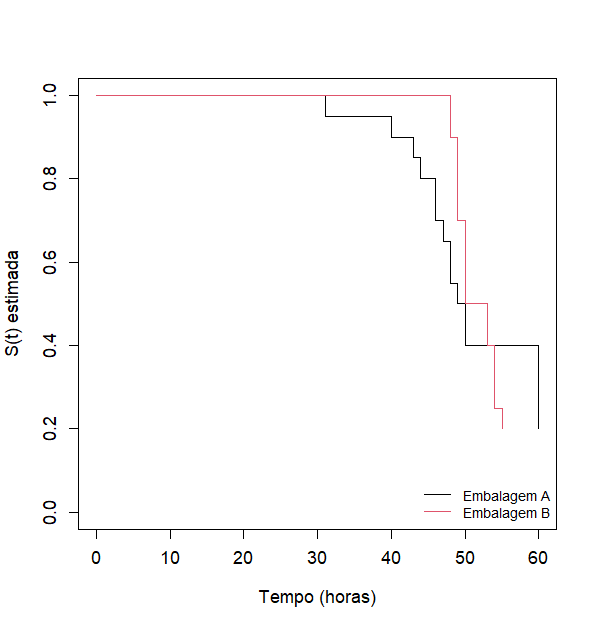
Na embalagem B, aparentemente, o produto dura por mais tempo. Note que a probabilidade de sobrevivência do produto na embalagem B até o tempo de 50 horas é acima de 80%, enquanto a embalagem A começa a decair a partir de 30 horas. Próximo das 50h, as curvas de sobrevivência se encontram e pode ser feita a seguinte pergunta: e se não existir diferença em ambas as curvas?

Desta forma, como o intuito é verificar se as curvas de sobrevida são iguais, é indicado o uso do teste log rank. Esse teste compara a diferença entre o número de eventos observados e o número de eventos esperados em cada tempo e pode ser usado para comparar duas ou mais curvas. Testa-se que não há diferença na sobrevivência entre os grupos (hipótese nula).

Como o p-valor foi 0,9, pode-se dizer que não há evidências para rejeitar a hipótese nula ao nível de 5% de significância. Isso quer dizer: não existe diferença entre as curvas de sobrevivência para os dois tipos de embalagens.

Quais são os modelos convencionais em Análise de Sobrevivência ?

Os modelos probabilísticos mais convencionais em análise de sobrevivência são: exponencial, Weibull e log-normal. Esses modelos possuem destaque devido às circunstâncias práticas.

A distribuição exponencial é o modelo mais usual para descrever o tempo de falha, e tem como propriedade a função de taxa de falha constante (observação velha quanto nova que ainda não observaram a falha, possuem a mesma probabilidade de falha em um tempo futuro). É relevante na descrição do tempo de vida de produtos e materiais na área da engenharia, voltada para o controle de qualidade desses produtos. Entretanto, também é possível o seu uso para estimar o tempo de vida de pacientes nos estudos clínicos.

A distribuição Weibull (Weibull, 1939) é bastante utilizada por biomédicos devido à propriedade da sua função de taxa de falha ser monótona, ou seja, esta função é constante, crescente ou decrescente.

Já a distribuição log-normal está atrelada aos tempos de vida de produtos e indivíduos, como semicondutores e isolação elétrica. As taxas de falha crescem, atingem um valor máximo e logo depois decrescem.

Cada distribuição possui sua respectiva função de sobrevivência e a utilização desses modelos deve ser analisada e planejada com cuidado para que não ocorra erros nas estimativas de sobrevivência e consequentemente nos resultados.

Uma das formas de comparar e selecionar esses modelos é através do método gráfico, em que se usam as curvas de sobrevivência e verifica-se qual modelo probabilístico melhor se ajusta a curva de sobrevivência do estimador de Kaplan-Meier.

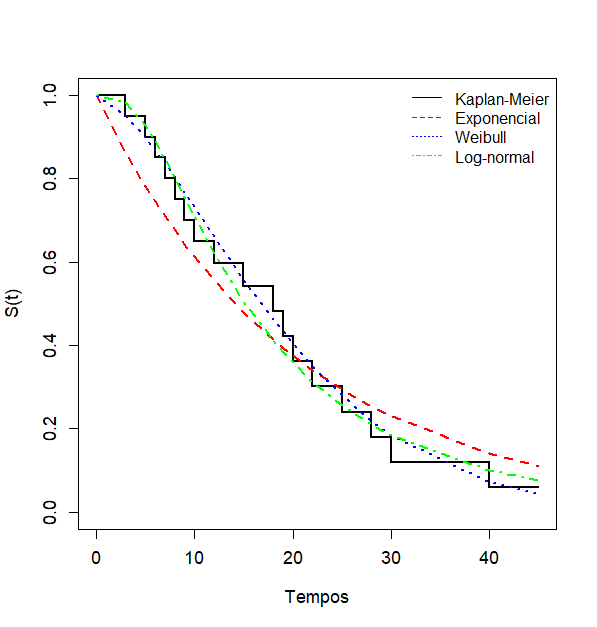
Através da figura dos modelos e suas respectivas curvas de sobrevivência versus a curva de sobrevivência de Kaplan-Meier, é possível observar qual modelo melhor se ajusta a referida curva. Assim, os modelos Weibull e log-normal melhor se adequam, apenas considerando a imagem. É importante salientar que o método gráfico é uma das formas de comparação de modelos para dados censurados.

Abordaremos outros modelos de sobrevivência e outros métodos de comparação como o teste de razão de verossimilhança e AIC em nossos futuros artigos. Então, não deixe de acompanhar o nosso Blog e nosso canal do Statplace no YouTube. Caso tenha alguma dúvida sobre análise de sobrevivência, não deixe de comentar!