A análise de séries temporais é um importante instrumento no entendimento do mercado e na formulação de planos de ação e estratégias. O histórico de uma variável pode ser utilizado na identificação de períodos de crescimento/decrescimento, sazonalidade e ainda para “prever” observações futuras.
Modelos de séries temporais são muito utilizados para avaliar o comportamento de uma variável ao longo do tempo. Uma sorveteria, por exemplo, tende a vender mais sorvete durante o verão, enquanto o mercado para as cafeterias costuma ser mais aquecido no inverno.
Seria possível “prever” a demanda por sorvete para o verão de 2020?
Na verdade, os modelos estatísticos para séries temporais utilizam o passado histórico da variável para projetar observações futuras. Dessa forma, se pode ter uma ideia, em média, de como a variável se comportará nos próximos períodos.
Séries Temporais: Autocorrelação
Os modelos estatísticos mais conhecidos e utilizados, como a Regressão Linear e o GLM, são adequados na modelagem de variáveis em que as observações são independentes. Em uma série temporal, não há como desconsiderar a estrutura de dependência das observações.
Por exemplo, a quantidade vendida de sorvete em fevereiro pode estar relacionada à quantidade vendida em janeiro, que por sua vez pode estar relacionada com a de dezembro e assim por diante. Dessa forma, a utilização desses modelos pode gerar resultados enviesados e que não refletem a realidade.
A autocorrelação é definida como uma observação num determinado instante está relacionada às observações passadas.
As observações podem estar autocorrelacionadas em diversas ordens. A autocorrelação de primeira ordem caracteriza séries onde uma observação está correlacionada com a observação imediatamente anterior (fevereiro e janeiro, por exemplo). A autocorrelação de segunda ordem caracteriza séries temporais onde uma observação está correlacionada com as observações a 2 unidades de tempo no passado (fevereiro e dezembro, por exemplo).
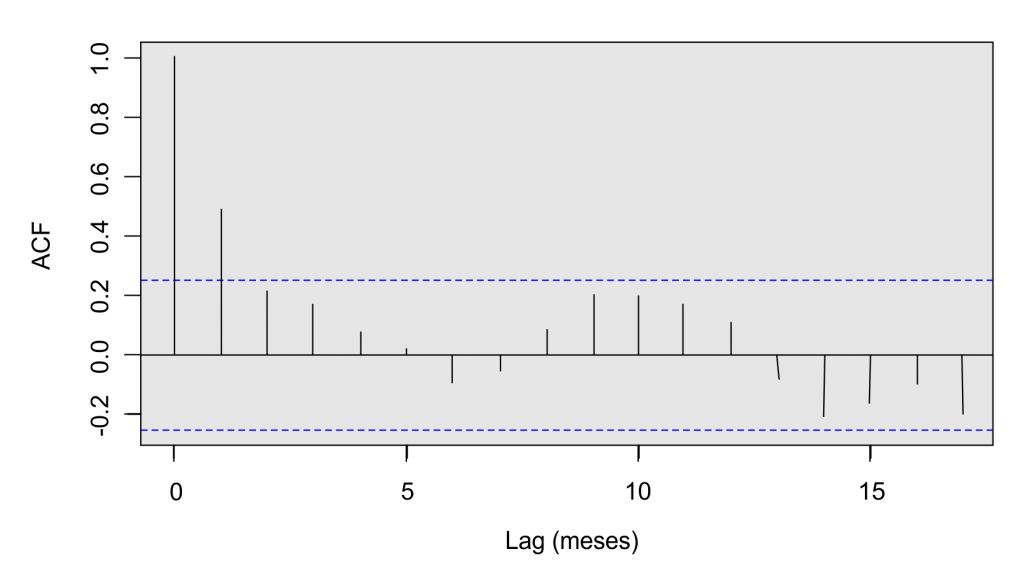
A identificação da autocorrelação é feita através da Função de Autocorrelação (ACF – Autocorrelation Function), mostrada abaixo. Além disso, testes como o de Durbin Watson auxiliam na identificação da autocorrelação de primeira ordem.
No exemplo de ACF mostrado abaixo a significância da ordem de autocorrelação é avaliada através dos intervalos de confiança (em azul). Dessa forma, esta série possui autocorrelação de primeira ordem, uma vez que o ponto no lag 1 é significativo. No R, a autocorrelação no lag 0 é sempre igual a 1, por default.
Séries Temporais: Tendência
A tendência de uma série temporal é definida como um padrão de crescimento/descrecimento da variável em um certo período de tempo.
Existem testes específicos para a identificação da tendência, como o Teste de Wald e o de Cox-Stuart. Entretanto, uma técnica muito utilizada é o ajuste de uma Regressão Linear Simples para a identificação da inclinação da reta de tendência.
Vale lembrar que o ajuste da Regressão Linear, neste caso, pode levar a resultados enviesados e, para evitar este problema, estimadores robustos à autocorrelação podem ser utilizados. Este tópico será tratado futuramente em nossas publicações.
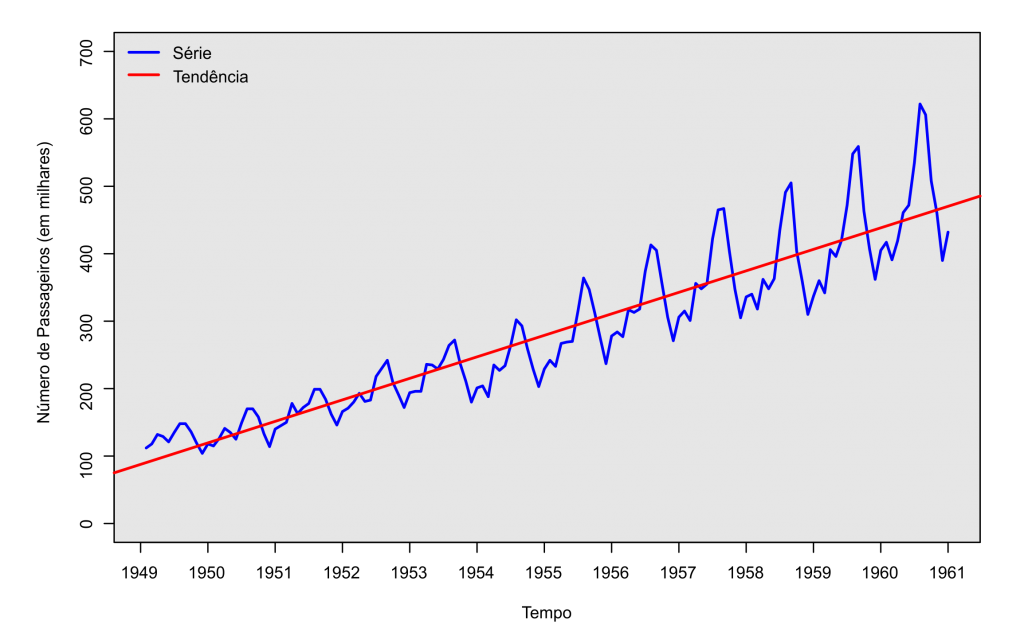
No exemplo abaixo, consideramos os dados referentes ao número de passageiros internacionais no transporte aéreo entre os anos de 1949 e 1961. Pode-se observar uma clara tendência crescente na série ao longo dos anos.
Séries Temporais: Sazonalidade
A sazonalidade pode ser definida como padrões de comportamento que se repetem em específicas épocas do ano. Por exemplo, o número de passageiros que utilizam o transporte aéreo geralmente é maior em períodos de férias escolares do que nos demais meses do ano, fato que pode ser verificado na imagem apresentada anteriormente.
A sazonalidade, muitas vezes, pode ser identificada de maneira visual. Uma das técnicas formais utilizadas é a identificação de autocorrelações significativas de determinada ordem. Por exemplo, se existe uma sazonalidade anual em uma série, a autocorrelação de ordem 12 geralmente é significativa.
Séries Temporais: Estacionariedade
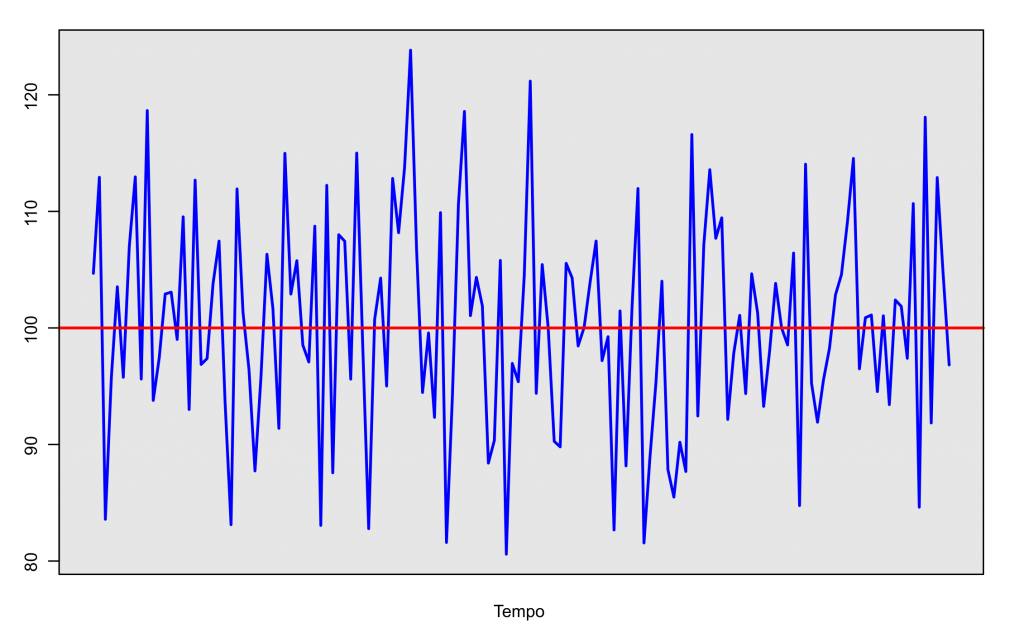
A estacionariedade é um importante conceito na modelagem de séries temporais e é caracterizada por uma variável que se comporta de forma aleatória ao longo do tempo ao redor de uma média constante.
Basicamente, séries temporais que possuem tendência e/ou sazonalidade não são estacionárias e é necessário o uso de técnicas adequadas a tal situação. Na imagem abaixo mostramos um exemplo de uma série estacionária.
Após o entendimento do comportamento da série e a identificação dos elementos é possível verificar qual o modelo mais adequado.
Para mais informações sobre as características das series temporais, entre em contato com nossos Data Talkers. Não deixe de se registrar em nosso blog para acompanhar nossas publicações.
Artigo desenvolvido com a colaboração de Leonardo Gonçalves.




7 comentários em “Características das séries temporais”
Muito oportuno este texto. Apresenta de forma clara um conceito que pra alguns é muito complexo. Obrigada e boa sorte.
Valeu Ester, ficamos felizes com o feedback! 😀
Caso eu queira comparar duas series temporais, uma a respeito da população e outra com amostra, qual o teste indicado para verificar se existem semelhança entre elas?
É difícil dizer, precisamos entender melhor os dados e o problema, mas você poderia ver a possibilidade de ajustar modelos de cointegração ou, dependendo da pergunta, aplicar um teste de Wilcoxon ou t pareado, para ver se existe diferença de médias entre as séries. Esse é um caminho bem simples e possível. Se você quiser se aprofundar nessa investigação entra em contato com a gente por telefone ou email!
Então me deixa ver se entendi, para se usar modelos de regressão linear em series temporais , elas precisam ser estacionárias?
Marcelo, as séries temporais que possuem tendência e/ou sazonalidade não são estacionárias. Nesse caso, é necessário o uso de técnicas adequadas à situação.
Se a relação entre o valor e o tempo for linear e a dispersão dos dados em relação à tendência for pequena e não aumentar com o tempo, é possível aplicar regressão linear com resultados adequados. Mas para o caso da segunda figura, em que a dispersão está aumentando com o tempo, é melhor aplicar técnicas mais adequadas.