A PCA é um método estatístico multivariado que foi introduzido por Karl Pearson em 1901.
Imagine um grande conjunto de dados com variáveis possivelmente correlacionadas. A necessidade de analisar esse banco de dados pode gerar algumas dúvidas:
- Se existem muitas variáveis como podemos explorar esses dados?
- Quais variáveis são mais importantes?
O foco é construir combinações lineares com as variáveis originais para reduzir dimensão. Essas combinações lineares são chamadas de componentes principais. Portanto, deseja-se reduzir o número de variáveis a serem avaliadas e interpretar as componentes principais criadas.
Se o banco de dados possui p variáveis, então é possível obter até p componentes principais. Mas, como a intenção é reduzir dimensão, aconselha-se contar com k (k < p) componentes. A informação contida nas p variáveis originais é substituída pela informação das k componentes.
Basicamente, deseja-se:
- identificar padrões ocultos no conjunto de dados;
- reduzir dimensão removendo ruídos.
Fatos importantes:
- as componentes principais são não correlacionadas;
- a normalidade multivariada dos dados NÃO é um requisito para utilizar a PCA. No entanto, caso os dados apresentem distribuição de probabilidade normal multivariada, as componentes principais são independentes e tem distribuição normal univariada.
Exemplos de utilização
- Avaliação da reação de pacientes à radioterapia (Johnson; Wichern – 2002)
- Comparação de estabelecimentos comerciais de Belo Horizonte, MG (Mingoti; Silva – 1997)
- Controle de qualidade de processos (Kourti; MacGregor – 1996)
- Estudos de calibração (Fisher; Mara – 1986)
Como obter as componentes principais?
Podemos extrair as componentes a partir da matriz de covariâncias ou da matriz de correlação.
- Matriz de covariância:
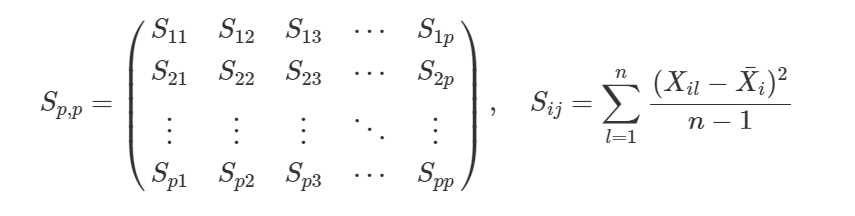
- Matriz de correlação:
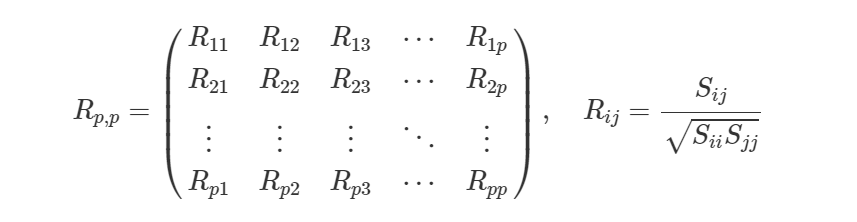
Se os dados forem transformados deve-se utilizar a matriz de covariâncias das variáveis transformadas. Quando as variáveis são padronizadas (subtrair a média e dividir pelo desvio-padrão) a matriz de covariâncias dos dados padronizados equivale à matriz de correlação das variáveis originais.
Definições importantes
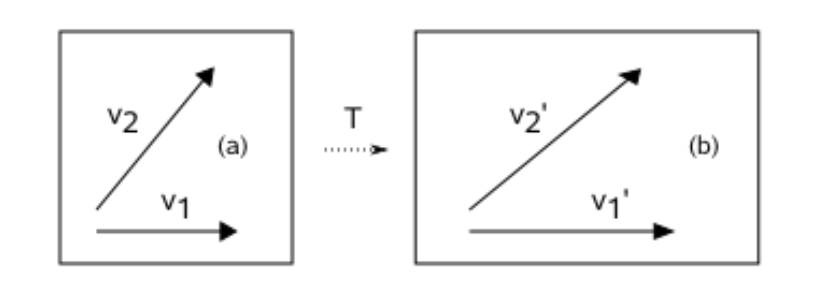
Na imagem (a) tem-se 2 vetores: v1 e v2. Ao transformar (a) em (b) o vetor v2 sofre uma mudança de magnitude e direção, já o vetor v1 sofre apenas uma mudança de magnitude. Essa mudança em v1 pode ser dada pela multiplicação de determinado valor (escalar = λ1).
- v′1 é um autovetor da transformação
- O escalar λ1 é o autovalor associado a v′1
Portanto, autovalores e autovetores são definicões relacionadas à transformações lineares.
Como o banco de dados possui p variáveis tem-se p autovalores, λ1 ≥ λ2 ≥ ⋯ ≥ λp, da matriz de covariâncias (ou correlação) com os respectivos p autovetores normalizados e1, e2, ⋯, ep.
- X = (X1 X2 ⋯ X2p)′: vetor aleatório (dados)
- μ = (μ1 μ2 ⋯ μp)′: vetor de médias
- Σpxp: matriz de covariâncias
A j-ésima (j = 1, 2, ⋯, p) componente principal da matriz de covariâncias (ou correlação) é definida como:
Yj = e′j X =e j1 X1 + ej2 X2 + ⋯ + ejp Xp
- OBS: Xi é uma variável do banco de dados com n observações.
Resuldados:
E[Yj] = e′j μ = ej1 μ1 + ej2 μ2 + ⋯ + ejp μp
Var[Yi] = e′j Σpxp ej = λj
Lembre-se que λ1 ≥ λ2 ≥ ⋯ ≥ λp, logo, a 1ª componente é a de maior variabilidade e a p-ésima é a de menor.
Se, a variância da j-ésima componente principal corresponde a λj, então, a variância total de X corresponde a soma dos autovalores (∑pi=1 λi). Portanto, a proporção da variância total de X que é explicada pela j-ésima componente principal é dada por:
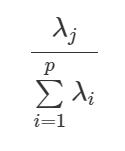
Além disso, a proporção total que é explicada pelas k primeiras componentes principais é definida como:
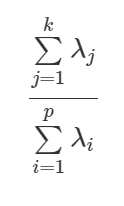
Como escolher o número k?
O número k de componentes principais pode ser escolhido a partir de vários critérios. Alguns deles são:
1. Manter um número de componentes k que conjuntamente representam uma determinada porcentagem da variância total;
2. Caso seja usada a matriz de correlação, manter apenas as componentes com autovalor ^λi≥1 (Critério de Kaiser, 1958);
3. Interpretação, a escolha de k pode ser definida pela natureza prática das componentes.
Aplicação e Script no R
Carregando os pacotes necessários:
library(tidyverse) # Para manipular os dados
library(stats) # Para PCA
library(factoextra) # Para criar alguns gráficosDescrição da base de dados mtcars
A base de dados mtcars (revista Motor Trend de 1974) descreve o consumo de combustível e 10 aspectos do design e desempenho de 32 automóveis.
Ao todo há 11 diferentes variáveis:
data("mtcars")
mtcars <- mtcars %>% rename(
"milhas_galao" = "mpg", # consumo de combustível em milhas por galão
# carros mais potentes e mais pesados tendem a consumir mais combustível
"cilindros" = "cyl", # número de cilindros
# carros mais potentes geralmente têm mais cilindros
"deslocamento" = "disp", # volume combinado dos cilindros do motor
"potencia_bruta" = "hp", # potência gerada pelo carro
"relacao_et" = "drat", # relação do eixo traseiro
# valores mais altos diminuirão a eficiência do combustível
"peso" = "wt", #(1.000 libras)
"tempo_14" = "qsec", # tempo de 1/4 de milha, velocidade e aceleração dos carros
"forma_motor" = "vs", # 0 = forma de V e 1 = reto (mais comum)
"transmissao" = "am", # 0 = automática e 1 = manual
"marchas" = "gear", # número de marchas para frente
# carros esportivos tendem a ter mais marchas
"carburador" = "carb" # número de carburadores, associados a motores mais potentes
)
head(mtcars)## milhas_galao cilindros deslocamento potencia_bruta relacao_et
## Mazda RX4 21.0 6 160 110 3.90
## Mazda RX4 Wag 21.0 6 160 110 3.90
## Datsun 710 22.8 4 108 93 3.85
## Hornet 4 Drive 21.4 6 258 110 3.08
## Hornet Sportabout 18.7 8 360 175 3.15
## Valiant 18.1 6 225 105 2.76
## peso tempo_14 forma_motor transmissao marchas carburador
## Mazda RX4 2.620 16.46 0 1 4 4
## Mazda RX4 Wag 2.875 17.02 0 1 4 4
## Datsun 710 2.320 18.61 1 1 4 1
## Hornet 4 Drive 3.215 19.44 1 0 3 1
## Hornet Sportabout 3.440 17.02 0 0 3 2
## Valiant 3.460 20.22 1 0 3 1Para calcular as componentes principais somente as 9 variáveis numéricas serão consideradas.
# Filtrando variáveis númericas
dados_pca <- mtcars[,c(1:7, 10, 11)]
# Calculando o desvio padrão das variáveis
sapply(dados_pca, sd)## milhas_galao cilindros deslocamento potencia_bruta relacao_et
## 6.0269481 1.7859216 123.9386938 68.5628685 0.5346787
## peso tempo_14 marchas carburador
## 0.9784574 1.7869432 0.7378041 1.6152000Obtendo as componentes
A função prcomp permite obter as componentes de forma simples.
# PCA com a matriz de covariâncias
pca_cov <- prcomp(dados_pca)
summary(pca_cov)## Importance of components:
## PC1 PC2 PC3 PC4 PC5 PC6 PC7
## Standard deviation 136.532 38.14735 3.06642 1.27492 0.90474 0.64734 0.3054
## Proportion of Variance 0.927 0.07237 0.00047 0.00008 0.00004 0.00002 0.0000
## Cumulative Proportion 0.927 0.99938 0.99985 0.99993 0.99997 0.99999 1.0000
## PC8 PC9
## Standard deviation 0.2859 0.2159
## Proportion of Variance 0.0000 0.0000
## Cumulative Proportion 1.0000 1.0000O desvio padrão (Standard deviation) da j-ésima componente corresponde a √λj.
Como as variáveis estão em diferentes escalas, o mais adequado é utilizar a matriz de correlação.
# PCA com a matriz de correlação (variáveis padronizadas)
pca_corr <- prcomp(dados_pca, center = TRUE, scale = TRUE)
summary(pca_corr)## Importance of components:
## PC1 PC2 PC3 PC4 PC5 PC6 PC7
## Standard deviation 2.3782 1.4429 0.71008 0.51481 0.42797 0.35184 0.32413
## Proportion of Variance 0.6284 0.2313 0.05602 0.02945 0.02035 0.01375 0.01167
## Cumulative Proportion 0.6284 0.8598 0.91581 0.94525 0.96560 0.97936 0.99103
## PC8 PC9
## Standard deviation 0.2419 0.14896
## Proportion of Variance 0.0065 0.00247
## Cumulative Proportion 0.9975 1.00000fviz_eig(pca_corr)
Interpretação:
A 1ª componente explica 62,84% da variância total dos dados. Portanto, quase 2/3 das informações contidas nas 9 variáveis do banco de dados podem ser encapsulada apenas nessa componente. A 2ª componente explica 23,13% da variância total. Com apenas 2 componentes 85,98% da variância dos dados é explicada.
# Coeficientes das componentes principais (autovetores da matriz de correlação)
summary(pca_corr)$rotation #Pode-se trocar os sinais## PC1 PC2 PC3 PC4 PC5
## milhas_galao -0.3931477 0.02753861 -0.22119309 -0.006126378 -0.3207620
## cilindros 0.4025537 0.01570975 -0.25231615 0.040700251 0.1171397
## deslocamento 0.3973528 -0.08888469 -0.07825139 0.339493732 -0.4867849
## potencia_bruta 0.3670814 0.26941371 -0.01721159 0.068300993 -0.2947317
## relacao_et -0.3118165 0.34165268 0.14995507 0.845658485 0.1619259
## peso 0.3734771 -0.17194306 0.45373418 0.191260029 -0.1874822
## tempo_14 -0.2243508 -0.48404435 0.62812782 -0.030329127 -0.1482495
## marchas -0.2094749 0.55078264 0.20658376 -0.282381831 -0.5624860
## carburador 0.2445807 0.48431310 0.46412069 -0.214492216 0.3997820
## PC6 PC7 PC8 PC9
## milhas_galao 0.72015586 -0.38138068 -0.12465987 0.11492862
## cilindros 0.22432550 -0.15893251 0.81032177 0.16266295
## deslocamento -0.01967516 -0.18233095 -0.06416707 -0.66190812
## potencia_bruta 0.35394225 0.69620751 -0.16573993 0.25177306
## relacao_et -0.01536794 0.04767957 0.13505066 0.03809096
## peso -0.08377237 -0.42777608 -0.19839375 0.56918844
## tempo_14 0.25752940 0.27622581 0.35613350 -0.16873731
## marchas -0.32298239 -0.08555707 0.31636479 0.04719694
## carburador 0.35706914 -0.20604210 -0.10832772 -0.32045892No caso em que todos os coeficientes apresentarem o mesmo sinal (positivo OU negativo) a componente é chamada de índice global. Quando os sinais são opostos a componente é chamada de índice comparativo.
^Y1 = −0.393 Z1 + 0.403 Z2 + 0.397 Z3 + 0.367 Z4 − 0.312 Z5 + 0.373 Z6 − 0.224 Z7 − 0.209 Z8 + 0.245 Z9
^Y1 = 0.393 Z1 − 0.403 Z2 − 0.397 Z3 − 0.367 Z4 + 0.312 Z5 − 0.373 Z6 + 0.224 Z7 + 0.209 Z8 − 0.245 Z9
- OBS: Zi é a variável i padronizada.
Interpretação PC1:
Em geral, os coeficientes estão equilibrados (todos estão relativamente próximos), sendo que, a variável Z2 apresentou o maior peso (-0.403). Além disso, trata-se de um índice de comparação entre os seguintes grupos de variáveis:
- Grupo 1 – Z1, Z5, Z7 e Z8 (coeficientes positivos)
- Grupo 2 – Z2, Z3, Z4, Z6 e Z9 (coeficientes negativos)
Quanto maior o valor das variáveis do Grupo 1, maior o valor do escore de ^Y1.
Quanto maior o valor das variáveis do Grupo 2, menor o valor do escore de ^Y1.
Escores
Cada automovel tem 1 escore para cada componente principal.
summary(pca_corr)$x## PC1 PC2 PC3 PC4 PC5
## Mazda RX4 -0.66422351 1.1734476 -0.20431724 -0.12601751 0.75200784
## Mazda RX4 Wag -0.63719807 0.9769448 0.11077779 -0.08567709 0.65668822
## Datsun 710 -2.29973601 -0.3265893 -0.21014955 -0.10862524 -0.07622329
## Hornet 4 Drive -0.21529670 -1.9768101 -0.32946822 -0.30806225 -0.24391787
## Hornet Sportabout 1.58697405 -0.8287285 -1.03299254 0.14738418 -0.22270405
## Valiant 0.04960512 -2.4466838 0.11177774 -0.87154914 -0.12574876
## Duster 360 2.71439677 0.3610529 -0.65206041 0.09633337 0.29674234
## Merc 240D -2.04370658 -0.8006412 0.84898795 -0.27451338 -0.26307848
## Merc 230 -2.29506729 -1.3056004 1.96848450 0.05055875 -0.45988113
## Merc 280 -0.38252133 0.5811211 0.88632274 0.07026946 0.45835852
## Merc 280C -0.36652708 0.4121971 1.14860950 0.06150898 0.48309076
## Merc 450SE 1.88466875 -0.7241198 -0.20604588 -0.21856675 0.27996207
## Merc 450SL 1.67107231 -0.7144354 -0.32644071 -0.28933625 0.28061777
## Merc 450SLC 1.77692371 -0.8411687 -0.08557921 -0.28421711 0.34961695
## Cadillac Fleetwood 3.64958983 -0.9480878 0.88315862 0.21645793 -0.34788247
## Lincoln Continental 3.71033756 -0.8426945 0.93230325 0.34099021 -0.34260485
## Chrysler Imperial 3.33196300 -0.4805609 0.67061959 0.65189724 -0.43940743
## Fiat 128 -3.45236266 -0.4327074 -0.22604214 0.10018032 -0.33470301
## Honda Civic -3.85477722 0.7084152 -0.22670973 1.19340342 0.53954318
## Toyota Corolla -3.85488283 -0.3872111 -0.25488964 0.21962306 -0.30372397
## Toyota Corona -1.90375523 -1.5725638 0.06620424 0.07989679 0.50126570
## Dodge Challenger 1.80402354 -1.1340965 -1.00776416 -0.58796239 0.09903732
## AMC Javelin 1.46483534 -0.9777629 -0.76680342 -0.03308788 0.26871378
## Camaro Z28 2.60135738 0.7649595 -0.48915140 0.95247550 0.53065965
## Pontiac Firebird 1.87424485 -0.9791561 -0.89787633 0.22438738 -0.50770999
## Fiat X1-9 -3.14830645 -0.2552569 -0.36230545 0.06406082 0.03361267
## Porsche 914-2 -2.77939557 1.6373369 -0.35969974 0.31886540 -0.43251030
## Lotus Europa -2.90895427 1.3962368 -0.91635036 -0.90254314 -0.75861156
## Ford Pantera L 1.54812696 3.0206982 -0.51945216 0.86560850 -0.86048411
## Ferrari Dino 0.08049995 2.8346567 0.34481747 -1.14659658 0.29944552
## Maserati Bora 2.96252801 3.9993896 0.70296512 -0.73000448 -0.22756074
## Volvo 142E -1.90443632 0.1084190 0.39906976 0.31285789 0.11738974
## PC6 PC7 PC8 PC9
## Mazda RX4 -0.12506777 -0.42357334 -0.003259165 -0.167051112
## Mazda RX4 Wag -0.06619437 -0.44849307 0.056643244 -0.071592094
## Datsun 710 -0.56693648 0.38612406 -0.202035744 0.114505030
## Hornet 4 Drive 0.08382435 0.03299362 -0.023714111 -0.145255757
## Hornet Sportabout 0.18280435 -0.05793795 0.152342587 -0.154646072
## Valiant -0.23043022 0.22451528 0.098663134 -0.004233901
## Duster 360 0.27763557 0.44227307 -0.306373481 -0.186980810
## Merc 240D -0.19042527 -0.39416400 -0.187088365 -0.010461330
## Merc 230 0.20443847 0.53713423 0.413455512 -0.169005773
## Merc 280 -0.07984989 -0.26113412 0.204105964 0.110461785
## Merc 280C -0.16066456 -0.07979514 0.352641772 0.027108266
## Merc 450SE 0.17135058 -0.08914480 0.092140434 0.396034809
## Merc 450SL 0.33682412 0.03346598 0.182323579 0.196526577
## Merc 450SLC 0.13926264 0.20632469 0.295340402 0.147796262
## Cadillac Fleetwood -0.24002207 -0.31053111 -0.171865268 -0.251117818
## Lincoln Continental -0.22646211 -0.28589695 -0.239313268 -0.028994385
## Chrysler Imperial 0.31045750 -0.38304409 -0.359765688 0.223097923
## Fiat 128 0.57303421 -0.24650594 -0.066340528 0.220271421
## Honda Civic 0.37207104 -0.20055288 0.087333576 -0.241702175
## Toyota Corolla 0.83750899 -0.10186868 0.104053562 0.042833437
## Toyota Corona -0.07212137 0.74680802 -0.408144457 -0.082722856
## Dodge Challenger -0.33920894 -0.14045443 0.156086022 -0.050247532
## AMC Javelin -0.31479492 0.03753417 0.370979414 -0.043466032
## Camaro Z28 0.05970074 0.38212238 -0.289612990 0.082069840
## Pontiac Firebird 0.20785973 -0.32709161 0.027471038 -0.130958896
## Fiat X1-9 -0.09586730 0.10352270 -0.020876499 0.021084764
## Porsche 914-2 -0.69006515 -0.26313120 -0.105695694 0.085027267
## Lotus Europa 0.05473409 -0.03491081 -0.236552376 -0.046341050
## Ford Pantera L -0.50704173 0.37940892 0.548070377 0.053196712
## Ferrari Dino -0.08124583 -0.26924964 -0.123537656 -0.047915313
## Maserati Bora 0.65580986 0.49422807 -0.082329298 -0.053112079
## Volvo 142E -0.48091826 0.31102454 -0.315146031 0.165790892Gráficos
Interpretação geral dos gráficos:
Os quadrantes com circulos azuis indicam que uma componente explicou mais as variáveis presentes nesse quadrante do que a outra componente.
# Gráfico de indivíduos (automóveis)
fviz_pca_ind(pca_corr,
col.ind = "cos2", #Cor pela qualidade de representação
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
repel = TRUE, # Texto não sobreposto
legend.title = "Representação"
)
# Gráfico das variáveis
fviz_pca_var(pca_corr,
col.var = "contrib", # Cor por contribuições para o PC
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
repel = TRUE,
legend.title = "Contribuição"
)
# Gráfico das variáveis e indivíduos
fviz_pca_biplot(pca_corr, repel = TRUE,
col.var = "#2E9FDF", # cor das variáveis
col.ind = "#696969" # cor dos automoveis
)
# Trocando os nomes das categorias
mtcars <- mtcars %>% mutate(
forma_motor = case_when(forma_motor == 0 ~ "Forma V",
TRUE ~ "Forma reta"),
transmissao = case_when(transmissao == 0 ~ "Automática",
TRUE ~ "Manual")
)
fviz_pca_ind(pca_corr,
col.ind = mtcars$forma_motor, # cor por forma
palette = c("#00AFBB", "#FC4E07"),
addEllipses = TRUE,
ellipse.type = "confidence",
legend.title = "Forma do motor",
repel = TRUE
)
fviz_pca_ind(pca_corr,
col.ind = as.factor(mtcars$transmissao), # cor por transmissao
palette = c("#00AFBB", "#FC4E07"),
addEllipses = TRUE,
ellipse.type = "confidence",
legend.title = "Transmissão",
repel = TRUE
)
# Gráfico das variáveis e indivíduos
fviz_pca_biplot(pca_corr, repel = TRUE,
col.var = "black", # cor das variáveis
col.ind = as.factor(mtcars$transmissao), # cor dos automoveis
addEllipses = TRUE,
legend.title = "Transmissão"
)
Gostou desse artigo? Siga-nos nas redes sociais para saber sempre que lançarmos conteúdos novos.




4 comentários em “Análise de Componentes Principais (PCA): cálculo e aplicação no R”
Olá gostei do texto gostaria de saber quais informações(dados) de Banco ou Finança eu posso usar para aplicação de componentes principais.
Oi Adjilson! A ideia do uso do PCA é reduzir a dimensionalidade dos dados. Se a base de dados possui muitas variáveis, o objetivo do uso da PCA é explorar esses dados, reduzindo o número de variáveis a serem avaliadas, interpretar essas componentes sem que haja a perda de informação. Em relação a dúvida, seria interessante ter variáveis numéricas.
Olá, tudo bem?
O que fazer se algumas das variáveis apresentam dados faltantes?
Bom dia, Roger!
Depende. Não podemos excluir uma variável apenas porque ela apresenta dados faltantes. O mais indicado é avaliar a importância dessa variável para o estudo, bem como a quantidade de dados faltantes e o quanto eles estão impactando nos resultados.
Se for uma quantidade pequena de dados faltantes, é possível realizar as análises a depender do tipo de estudo. Caso contrário, é melhor avaliar os resultados considerando todas as observações (incluindo os NA) como também sem considerar os dados faltantes.